Futoshiki: an Answer Set Programming approach
Saturday, 23rd July, 2022
Futoshiki is a logic/number puzzle. Each row and column must contain all the numbers 1-9 (or whatever the size of the grid); the greater-than signs between some cells dictate that the number in one cell should be greater than its neighbour.
Here’s a question and solution from futoshiki.org:
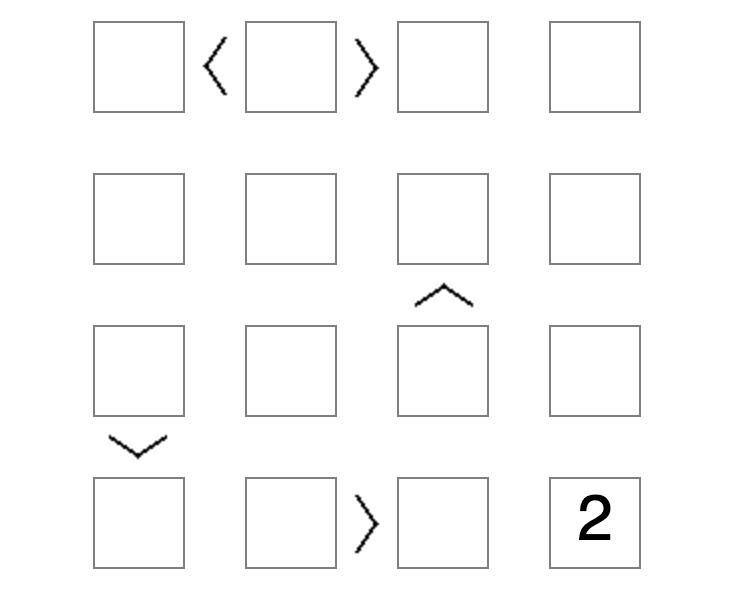

This can be very simply implemented in clingo. Encoding the rules like this:
number(1..n).
cell(R, C) :- number(R), number(C).
% each cell has one number
1 { cell_has_number(R, C, N) : number(N) } 1 :- cell(R, C).
% same numbers may not share row or column
:- cell_has_number(R, C1, N), cell_has_number(R, C2, N), C1 != C2.
:- cell_has_number(R1, C, N), cell_has_number(R2, C, N), R1 != R2.
% greater than constraint
A > B :- greater_than(R1,C1, R2,C2),
cell_has_number(R1,C1, A),
cell_has_number(R2,C2, B).
#show cell_has_number/3.
Encode for example the question grid above like this:
#const n = 4. cell_has_number(4,4, 2). greater_than(1,2, 1,1). greater_than(1,2, 1,3). greater_than(3,3, 2,3). greater_than(3,1, 4,1). greater_than(4,2, 4,3).
Run like this (output tidied for readability):
$ clingo futoshiki.lp futoshiki-grid4.lp 0
clingo version 5.5.0
Reading from futoshiki.lp ...
Solving...
Answer: 1
cell_has_number(1,1,2)
cell_has_number(1,2,3)
cell_has_number(1,3,1)
cell_has_number(1,4,4)
cell_has_number(2,1,4)
cell_has_number(2,2,1)
cell_has_number(2,3,2)
cell_has_number(2,4,3)
cell_has_number(3,1,3)
cell_has_number(3,2,2)
cell_has_number(3,3,4)
cell_has_number(3,4,1)
cell_has_number(4,1,1)
cell_has_number(4,2,4)
cell_has_number(4,3,3)
cell_has_number(4,4,2)
SATISFIABLE
Models : 1
Calls : 1
Time : 0.003s (Solving: 0.00s 1st Model: 0.00s Unsat: 0.00s)
CPU Time : 0.003s
Solving a Logic Puzzle with Clingo
Wednesday, 26th August, 2020
I am working through the exercises in Vladimir Lifschitz’ Answer Set Programming (Springer, 2019). Section 3.2 shows a clingo encoding of one of those logic problems:
Each of four men owns a different species of exotic pet. Here is what we know about them:
…
We would like to find the full name of the person who owns the jackal.
I thought I would try and encode a similar puzzle from a magazine — a puzzle found in the wild! Logic Problems from Puzzler Media is my favourite and this puzzle was from the May issue (No. 429):
The code:
%%%% Boys in the Hood
%%%% The world.
episode(1..5).
victim(friar_tuck; little_john; maid_marian; much; will_scarlet).
location(inn; dungeon; lodge; gaol; stocks).
disguise(abbot; shepherd; phantom; prince_john; washerwoman).
%% For each Episode, there is one (V,L,D) combination,
%% and the four variables together make a story.
{ story(E, V, L, D) :
victim(V),
location(L),
disguise(D) } = 1 :-
episode(E).
%% Each victim, location and disguise appears in one episode only.
E1 = E2 :- story(E1, V, _, _), story(E2, V, _, _).
E1 = E2 :- story(E1, _, L, _), story(E2, _, L, _).
E1 = E2 :- story(E1, _, _, D), story(E2, _, _, D).
%%%% Clue 1
%% "Prince John" rescued a victim from the dungeon, ...
D = prince_john :-
story(_, _, dungeon, D).
%% ... this was in the next episode after Little John's appearance.
E2 = E1 + 1 :-
story(E1, little_john, _, _),
story(E2, _, dungeon, _).
%%%% Clue 2
%% Friar Tuck was rescued from the inn.
L = inn :-
story(_, friar_tuck, L, _).
%%%% Clue 3
%% The "washerwoman" appeared in episode 2.
D = washerwoman :-
story(2, _, _, D).
%%%% Clue 4
%% Much the miller's son appeared in a later episode than the "abbot", ...
E1 < E2 :-
story(E1, _, _, abbot),
story(E2, much, _, _).
%% ... but an earlier episode than the rescue from the lodge.
E1 < E2 :-
story(E1, much, _, _),
story(E2, _, lodge, _).
%%%% Clue 5
%% The "phantom horseman" rescued Will Scarlet, ...
V = will_scarlet :-
story(_, V, _, phantom).
%% ... in a later episode than the rescue from the gaol.
E1 < E2 :-
story(E1, _, gaol, _),
story(E2, will_scarlet, _, _).
%%%% Clue 6
%% The rescue from the stocks was in episode 3, ...
L = stocks :-
story(3, _, L, _).
%% ... and did not feature Will Scarlet.
:- story(3, will_scarlet, _, _).
%%%% Clue 7
%% The "shepherd" was the rescuer in the episode before Maid Marian's.
E2 = E1 + 1 :-
story(E1, _, _, shepherd),
story(E2, maid_marian, _, _).
%% Maid Marian was not the victim in episode 2.
:- story(2, maid_marian, _, _).
#show story/4.
(… and in a gist.)
After describing the four sets, the first constraint involves a set comprehension, or "choice rule" in ASP parlance:
{ story(E, V, L, D) :
victim(V),
location(L),
disguise(D) } = 1 :-
episode(E).
The form { p(X, Y) : q(X), r(Y) } describes a set — the set of facts p(X, Y) where q(X), r(Y) is true.
The form { ... } = n asserts that the cardinality of the set described is n.
Perhaps betraying my Prolog background, I initially tried to write things like (for Clue 2) …
story(_, friar_tuck, inn, _).
… which wouldn’t compile (unsafe anonymous variables), or …
story(E, friar_tuck, inn, D) :-
episode(E),
disguise(D).
… which didn’t work. Thinking of the clues as constraints rather than facts or predicates was the breakthrough, and the correct (or, at least, working) version, is concise and elegant:
L = inn :-
story(_, friar_tuck, L, _).
A fun little exercise on "real world" but still relatively tame data. Recommended!
To any Answer Set Programming experts reading: how could this program be improved?
